Exemple_C

Un exercice « Calculer »

Exercice
Trouver neuf termes consécutifs d’une suite arithmétique croissante dont la somme soit égale à

{63}

et dont la somme des carrés soit égale à

{981}

Cliquer ici pour voir/cacher le corrigé

On cherche les neuf termes sous la forme :

{a-4r,a-3r,a-2r,a-r,a+r,a+2r,a+3r,a+4r\text{\ où\ }r>0}

La somme

{S_1}

vaut

{9a}

donc la condition

{S=63}

donne

{a=7}

.
La somme des carrés est :

{\begin{array}{rl}S'&=(a-4r)^2+(a-3r)^2+(a-2r)^2+(a-r)^2\\&\qquad+(a+r)^2+(a+2r)^2+(a+3r)^2+(a+4r)^2\\\\&=9a^2+2r^2(16+9+4+1)=9a^2+60r^2\\\\&=441+60r^2\end{array}}

La condition

{S'=981}

donne

{60r^2=540}

donc

{r^2=9}

donc

{r=3}

.
On obtient donc la séquence :

{-5,-2,1,4,7,10,13,16,19}

Exercice
Tracer la courbe représentative de

{x\mapsto f(x) = \dfrac{\sqrt{x(x-2)}}{(x-1)^2}}

Cliquer ici pour voir/cacher le corrigé

Le domaine de définition de

{f}

est

{\mathcal{D}=]-\infty,0\,]\,\cup\,[\,2,+\infty[}

On a ${f'(x)=-\dfrac{x^2-2 x-1}{(x-1)^3\sqrt{(x-2) x}}}$ , pour ${x\in\mathcal{D'}=]-\infty,0\,[\,\cup\,]\,2,+\infty[}$ .

On remarque l’identité ${f(2-x)=\dfrac{\sqrt{(2-x)(-x)}}{(1-x)^2}=f(x)}$ .
Cela signifie que la droite verticale ${x=1}$ est axe de symétrie.
Il suffit donc de faire l’étude pour ${x\ge2}$ .

{P(x)=x^2-2 x-1}

s’annule en

{x=1-\sqrt2\lt 0}

{x=1+\sqrt2>2}

.
Ainsi

{\begin{cases}f'(x)>0\text{\ pour\ }2\lt x\lt 1+\sqrt2\\ f'(x)\lt 0\text{\ pour\ } x\gt 1+\sqrt2\end{cases}}

Sur ${[2,+\infty[}$ , la fonction ${f}$ atteint son maximum en ${f(1+\sqrt2)=\dfrac{1}{2}}$ .
Par croissance comparée, on a ${\displaystyle\lim_{x\to-\infty}f(x)=\displaystyle\lim_{x\to+\infty}f(x)=0^+}$ .
Il y a aux points ${(0,0}$ et ${(2,0)}$ une demi-tangente verticale dirigée vers les ${y>0}$ .
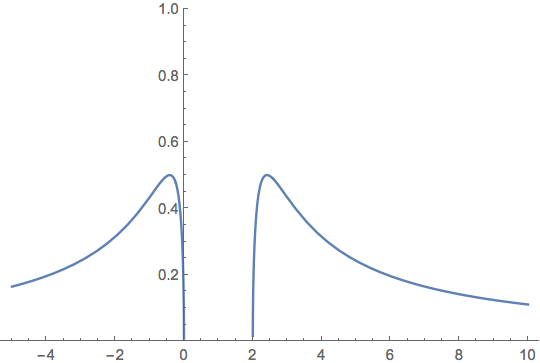
Voici l’allure de la courbe représentative :

Un exercice « Calculer »

Formulaire de contact