Comment préparer les maths des classes préparatoires scientifiques avec Mathpremium ?
Le site Mathpremium constitue le support qui accompagne les participants aux stages Trajectoire Prépa scientifique. Il contient des notes de cours et de très nombreux exercices corrigés.
- Les notes de cours représentent l’équivalent des trois premiers mois d’une « math sup », à un moment où on approfondit les notions et méthodes abordées en classe de Terminale. La lecture soignée de ces chapitres est un atout dans la perspective d’études en classe préparatoire scientifique.
- Chaque stage Trajectoire vient avec de très nombreux exercices de maths proposés par le responsable du stage, puis étudiés par le groupe. Le site mathpremium.fr reprend tous ces exercices mais aussi de nombreux autres qu’il est impossible de traiter dans le temps forcément limité du stage. Tous les exercices proposés sur ce site sont corrigés en détail.

Le lycée Henri IV, une prépa parisienne d’excellence

Le lycée Louis-le-Grand, une autre grande classe prépa scientifique
Nous proposons ici, en consultation libre, un aperçu du matériel pédagogique mis à disposition des stagiaires, afin que tous puissent se faire une idée de la qualité des documents proposés. Bien sûr il ne s’agit que d’une toute petite sélection de ce qui est proposé au fil des stages. Certains exercices figurant dans cet aperçu pourront sembler un peu difficiles à un élève de Terminale, mais il ne faut pas oublier que tous sont présentés et résolus en groupe sous la direction du responsable du stage (lui-même souvent professeur en classe préparatoire) et qu’ils préfigurent le niveau mathématique auquel vous devrez vous hisser après la Terminale.
Voici donc quelques extraits du contenu du site Mathpremium !
Une page du cours de Maths
Factorielle d’un entier
| Définition On pose {0!=1}, et pour tout {n} de {\mathbb{N}^{*}}, on note {n!=n\;(n-1)!}. Le symbole {n!} se lit « factorielle {n}« . |
Remarques :
- L’énoncé précédent est un exemple de définition récursive.
- Pour tout {n} de {\mathbb{N}^{*}}, l’entier {n!} est le produit des entiers de {1} à {n}, c’est-à-dire {n!=\displaystyle\prod_{k=1}^nk}
-
On retiendra les valeurs :
{\qquad 0!=1}, {1!=1}, {2!=2}, {3!=6}, {4!=24}, {5!=120}, {6!=720}, {7!=5040}. - L’entier {n!} désigne le nombre de permutations d’un ensemble à {n} éléments (c’est-à-dire de bijections de cet ensemble sur lui-même). Par exemple les {3!=6} permutations des lettres du mot {abc} sont : {abc}, {acb}, {bac}, {bca}, {cab} et {cba}.
-
Pour les grandes valeurs de {n}, on verra plus tard la formule de Stirling : {n!\sim n^{n}\text{e}^{-n}\sqrt{2\pi n}}.
La signification de {\sim} est que le quotient des deux expressions tend vers {1} quand {n} tend vers {+\infty}.
Par exemple, pour {n=20}, on a {\begin{cases}n!=2432902008176640000\\n^{n}\text{e}^{-n}\sqrt{2\pi n}\approx 2.42278684676\cdot 10^{18}\end{cases}}
Coefficients binomiaux
| Définition (combinaisons de p éléments parmi n) Soient {n} et {p} deux entiers, avec {0\le p\le n}. Soit {E} un ensemble fini possédant {n} éléments. On note {\dbinom{n}{p}} le nombre de sous-ensemble de {E} possédant {p} éléments. |
Remarques :
-
L’ensemble {E} dont il est question ici est évidemment sans importance.
Par exemple, dans l’ensemble {E=\{a,b,c,d,e\}}, il y a {10} parties à trois éléments, qui sont {\{a,b,c\}}, {\{a,b,d\}}, {\{a,b,e\}}, {\{a,c,d\}}, {\{a,c,e\}}, {\{a,d,e\}}, {\{b,c,d\}}, {\{b,c,e\}}, {\{b,d,e\}}, {\{c,d,e\}} - Le coefficient {\dbinom{n}{p}} se lit « {p} parmi {n}« .
-
Si {E} a {n} éléments, il y a dans {E} : une seule partie vide, donc {\dbinom{n}{0}=1}.
De même, il y a une seule partie à {n} éléments ({E} lui-même), donc {\dbinom{n}{n}=1}. - On étend la définition en posant {\dbinom{n}{p}=0} si {p\lt 0} ou {p>n} (ce qui est assez logique).
| Proposition Soient {n} et {p} deux entiers, avec {0\le p\le n}. On a l’égalité {\dbinom{n}{p}=\dfrac{n!}{p!\,(n-p)!}} |
Relations entre coefficients binomiaux
| Proposition On a les identités {\dbinom{n}{p}=\dbinom{n}{n-p}}, et {\dbinom{n}{p}=\dbinom{n-1}{p}+\dbinom{n-1}{p-1}}. |
La deuxième formule, avec {\dbinom{n}{0}=\dbinom{n}{n}=1}, permet de calculer les {\dbinom np} de proche en proche.
On place souvent les {\dbinom{n}{p}} dans un tableau triangulaire, de lignes et colonnes numérotées à partir de {0}.
Le coefficient {\dbinom{n}{p}} s’y place à l’intersection de la ligne d’indice {n} et de la colonne d’indice {p}.
Le tableau obtenu est connu sous le nom de « triangle de Pascal » :
{\begin{array}{c|c|c|c|c|c|c|c|c|}&p=0&p=1&p=2&p=3&p=4&p=5&p=6&\,\cdots\,\cr n=0&1& & & & & & &\cr n=1&1&1& & & & & &\cr n=2&1&2&1& & & & &\cr n=3&1&3&3&1& & & &\cr n=4&1&4&6&4&1& & &\cr n=5&1&5&10&10&5&1& &\cr n=6&1&6&15&20&15&6&1&\cr\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\ddots\cr n&\dbinom n0&\dbinom n1&\dbinom n2&\dbinom n3&\dbinom n4&\dbinom n5&\dbinom n6&\ddots\cr\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\ddots\cr\end{array}}
| Proposition On a les trois égalités : {\dbinom n{p+1}=\dfrac{n-p}{p+1}\,\dbinom np,\quad\dbinom np=\dfrac np\,\dbinom {n-1}{p-1},\quad \dbinom np=\dfrac n{n-p}\,\dbinom {n-1}p} |
| Proposition (Formule du binôme) Pour tous {x,y} de {\mathbb{C}}, et pour tout {n} de {\mathbb{N}} : {(x+y)^n=\displaystyle\sum_{k=0}^n\dbinom nk\,x^k\,y^{n-k}}. En particulier : {(1+x)^n=\displaystyle\sum_{k=0}^n\dbinom nk\,x^k}. |
En particulier, pour tous {x} et {y} de {\mathbb{C}} :
- {(x+y)^2=x^2+2xy+y^2}
- {(x-y)^2=x^2-2xy+y^2}
- {(x+y)^3=x^3+3x^2y+3xy^2+y^3}
- {(x-y)^3=x^3-3x^2y+3xy^2-y^3}
- {(x+y)^4=x^4+4x^3y+6x^{2}y^2+4xy^3+y^{4}}
- {(x-y)^4=x^4-4x^3y+6x^{2}y^2-4xy^3+y^{4}}
Un exercice « Raisonner »
Rappel : les rationnels sont les réels qui s’écrivent comme quotient de deux entiers, et les irrationnels sont tous autres.
|
Un exercice « Calculer »
Trouver neuf termes consécutifs d’une suite arithmétique croissante dont la somme soit égale à {63} et dont la somme des carrés soit égale à {981}. |
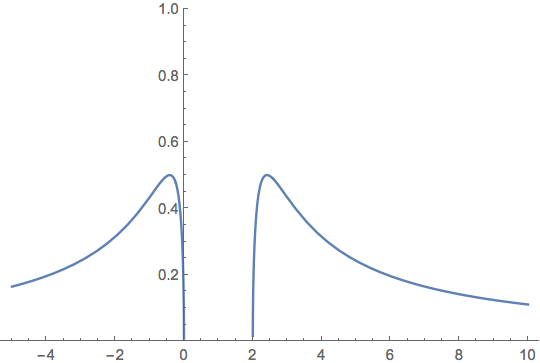
Tracer la courbe représentative de {x\mapsto f(x) = \dfrac{\sqrt{x(x-2)}}{(x-1)^2}} |
Deux exercices « Dénombrer »
|
|
Une page du cours Python
Branchements conditionnels if….
Pour dévier le flot des instructions en fonction de la valeur (vraie/fausse, non_nulle/nulle, non_vide/vide) d’une expression (appelée ici condition), Python met à notre disposition les clauses if, elif et else.
La clause if simple permet d’exécuter un bloc d’instructions si la condition est vraie :
if condition: # si condition est vraie
bloc_si_condition_vraie # alors on parcourt ce bloc
On peut rajouter une clause else (facultative, donc) pour exécuter un autre bloc si la condition est fausse :
if condition: # si condition est vraie
bloc_si_condition_vraie # on parcourt ce premier bloc
else: # sinon
bloc_si_condition_fausse # on parcourt ce second bloc
Plutôt que d’emboîter des clauses if, on peut utiliser une clause if suivie par une (des) clause(s) elif :
if condition1: # si condition1 est vraie
bloc1_si_C1_vraie # alors on exécute ce bloc1
elif condition2: # sinon si condition2 est vraie
bloc1_si_C1_fausse_et_C2_vraie
elif condition3: # sinon si condition3 est vraie
bloc3_si_C1C2_fausses_mais_C3_vraie
...
elif conditionN: # sinon si conditionN est vraie
blocN_si_CN_première_à_être_vraie
else: # (facultatif) conditions toutes fausses
bloc_else # alors on exécute ce bloc
Remarques :
- Dans toutes les constructions ci-dessus, au plus un bloc est parcouru;
- Ne pas oublier le caractère « deux points » qui termine chacune des lignes d’en-tête !!! ;
- Se souvenir que si un bloc se réduit à une instruction, on peut le placer directement après le « deux points ».
if x % 2: # comprendre "si x est non nul modulo 2"
print("x est impair")
elif x % 4: # x est pair, et on teste son reste modulo 4
print("x est pair, mais pas multiple de 4")
elif x % 8: # x multiple de 4, on teste son reste modulo 8
print("x multiple de 4, mais pas de 8")
else: # si on est là, x est multiple de 8
print("x est multiple de 8")
Complément : expressions conditionnelles
Python offre la possibilité de former des expressions dont l’évaluation est soumise à une condition.
La syntaxe est la suivante : expression1 if condition else expression2
Le résultat est bien sûr l’évaluation de expression1 si la condition est vraie, et sinon c’est celle de expression2.
On voit sur le deuxième exemple ci-dessous comment emboîter deux expressions conditionnelles.
>>> x = -1; print("x > 0" if x>0 else "x ≤ 0")
x ≤ 0
>>> x = 0; print("x > 0" if x>0 else "x < 0" if x<0 else "x = 0")
x = 0
Les répétitions inconditionnelles (for…)
Pour répéter un certain nombre de fois un bloc d’instructions, on utilisera la construction suivante :
for element in objet: # pour chaque élément de objet
bloc_d’instructions # on parcourt ce bloc
En fait, objet est ici est toute construction susceptible d’être parcourue : on pense bien sûr aux intervalles (range), mais aussi aux chaînes (parcourues caractère par caractère), aux listes, aux tuples, aux dictionnaires….
for k in range(10): # pour k=0, puis k=1, etc., k=9
bloc_d_instructions # on parcourt ce bloc
for x in 'abcdef': # pour x = 'a', x = 'b', etc., x = 'f'
bloc_d_instructions # on parcourt ce bloc
for x in [7, 1, 8, 3, 4]: # pour x = 7, x = 1, etc., x = 4
bloc_d_instructions # on parcourt ce bloc
Le bloc qui fait suite à l’instruction for peut contenir deux instructions particulières, souvent attachées à un test if :
- break provoque la sortie immédiate de la clause for.
- continue passe directement à l’étape suivante de la boucle (ce qui reste du bloc après continue est donc ignoré).
Les répétitions conditionnelles (while…)
Pour répéter un bloc d’instructions tant qu’une condition est réalisée, Python nous propose la clause while :
while condition: # tant que la condition est vraie
bloc_si_condition_vraie # alors on parcourt ce bloc
Quelques remarques classiques sur ce genre de construction :
- Si condition est fausse dès le départ, le bloc qui suit n’est jamais parcouru.
- Dans la plupart des cas, le bloc qui suit l’instruction d’en-tête while agit sur la condition, de sorte que celle-ci, vraie au départ, devient fausse et provoque la sortie de la clause.
- On peut écrire une clause while avec une condition toujours vraie (par exemple while 1: ou while True:) à condition (pour éviter une boucle infinie) de sortir par un autre moyen (notamment par break ou return).
Dans l’exemple ci-dessous, on illustre la clause while avec l’exemple classique de la suite dite de Syracuse.
Celle-ci est définie par une valeur initiale x0 et la règle suivante : si xn est pair alors xn+1 = xn/2 sinon xn+1 = 3xn + 1.
Une conjecture célèbre dit que l’un des xn vaut 1 (et la suite boucle alors sur les valeurs 1 → 4 → 2 → 1). On étudie ici le comportement très intéressant obtenu pour la valeur initiale x0 = 27 :
x = 27 # on part de la valeur 27
while x != 1: # tant que x est différent de 1
if x % 2 == 1 : # si x est impair,
x = 3*x+1 # on le remplace par 3x+1
else:
x = x // 2 # sinon, on le divise par 2
print(x, end=' ') # affiche x (sans passer à la ligne)
82 41 124 62 31 94 47 142 71 214 107 322 161 484 242 121 364 182
91 274 137 412 206 103 310 155 466 233 700 350 175 526 263 790
395 1186 593 1780 890 445 1336 668 334 167 502 251 754 377 1132
566 283 850 425 1276 638 319 958 479 1438 719 2158 1079 3238 1619
4858 2429 7288 3644 1822 911 2734 1367 4102 2051 6154 3077 9232
4616 2308 1154 577 1732 866 433 1300 650 325 976 488 244 122 61
184 92 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1
Le bloc qui fait suite à l’instruction while peut contenir deux instructions particulières, souvent attachées à un test if :
- break provoque la sortie immédiate de la clause while;
- continue ramène à l’évaluation de la condition (ce qui restait du bloc après continue est donc ignoré).
Fonctions récursives
Une fonction récursive est une fonction qui s’appelle elle-même, dans sa propre définition. Les deux exemples les plus simples sont l’algorithme d’Euclide et la fonction factorielle :
def pgcd(a,b): # algorithme d'Euclide
if b > 0: return pgcd(b, a % b)
else: return a
>>> pgcd(14814, 28440)
18
def fact(n): # calcule n!
if n <= 1: return 1
else: return n*fact(n-1)
>>> fact(10) # 10x9x8...x2x1
3628800
Un exercice « Programmer »
| Exercice (calculs dans une séquence) Dans cet exercice, L désigne une liste de nombres entiers ou flottants (ou même complexes).
|